Capítulo 5. Arrays

En los capítulos anteriores se han explorado con algunos ejemplos prácticos las nociones básicas sobre los elementos necesarios para hacer programas en Julia. Llegados a este punto, podemos revisitar y explorar en más profundidad cada uno de los conceptos estudiados, para sacarles el máximo provecho.

Empezaremos por el de las variables conocidas como arrays, entre las que se cuentan los vectores y las matrices que se introdujeron en el capítulo sobre series y tablas de datos. Los arrays son series organizadas de datos que pueden tener una, dos o más dimensiones. En el presente capítulo veremos más detalles sobre este tipo de variables, que son un elemento fundamental en la mayoría de cálculos numéricos, y por lo tanto conviene dominar desde un principio. Además, estos detalles servirán como introducción práctica a otros asuntos importantes para la programación en Julia.

Sintaxis para la creación de arrays

Vectores

Hay distintas formas de crear y componer arrays, algunas de las cuales ya se han visto en el capítulo 2. El caso más sencillo es el de los vectores (arrays unidimensionales), que se pueden definir escribiendo sus valores entre corchetes, separados por comas:

julia> numeros = [1,2,3,4]
4-element Vector{Int64}:
 1
 2
 3
 4

Por otro lado, la forma más general de crear arrays de cualquier dimensión es mediante la función cat (De "concatenar"), que utiliza el argumento con nombre dims para indicar en qué dimensión se añaden los valores introducidos. Por ejemplo, una forma alternativa (aunque menos práctica) de crear el vector numeros anterior es:

julia> cat(1,2,3,4, dims=1)
4-element Vector{Int64}:
 1
 2
 3
 4

Matrices

A la hora de trabajar con matrices, como ya se ha visto antes, se considera que la primera dimensión representa las filas, y la segunda representa las columnas. Por este motivo, una matriz se puede crear concatenando vectores a lo largo de una segunda dimensión (por columnas). Por ejemplo:

julia> sudoku = cat(
           [1,2,3,4],
           [4,3,1,2],
           [3,4,2,1],
           [2,1,4,3],
           dims=2)
4×4 Matrix{Int64}:
 1  4  3  2
 2  3  4  1
 3  1  2  4
 4  2  1  3

Como las matrices son un objeto de cálculo tan habitual, al igual que pasa con los vectores existen formas más prácticas de componerlas. La operación cat(a, b..., dims=2) se puede escribir como hcat(a, b...) –con "h" de "horizontal"–. Por lo tanto el sudoku anterior podría haberse escrito como:

julia> sudoku = hcat(
       [1,2,3,4],
       [4,3,1,2],
       [3,4,2,1],
       [2,1,4,3]
       )

Cuando los elementos a concatenar horizontalmente son más cortos, resulta aún más conciso escribirlos entre corchetes (como los vectores), pero separados por espacios en lugar de comas para indicar que se concatenan como una fila:

julia> fila = [1 2 3 4]
1×4 Matrix{Int64}:
 1  2  3  4

Así, tenemos otra forma de componer matrices, que es concatenando filas verticalmente. Esto se hace con la función vcat:

julia> sudoku2 = vcat(
           [1 2 3 4],
           [3 4 2 1],
           [4 3 1 2],
           [2 1 4 3]
           )
4×4 Matrix{Int64}:
 1  2  3  4
 3  4  2  1
 4  3  1  2
 2  1  4  3

Existen dos alternativas abreviadas de vcat usando corchetes: una es separando los elementos a concatenar con punto y coma, y la otra separándolos por cambios de línea, sin ningún otro separador. Así pues, este segundo sudoku podría haberse escrito de las dos siguientes maneras:

julia> [
         [1 2 3 4];
         [3 4 2 1];
         [4 3 1 2];
         [2 1 4 3]
       ]

julia> [
         [1 2 3 4]
         [3 4 2 1]
         [4 3 1 2]
         [2 1 4 3]
       ]

Y una forma más de componer matrices, especialmente práctica en estos casos en los que todos los valores son escalares breves de escribir, es mediante la operación combinada de concatenación horizontal y vertical. La función correspondiente es hvcat, y su forma abreviada utiliza una sola pareja de corchetes para todo el conjunto de datos, y los mismos separadores entre elementos que se emplean para la concatenación horizontal y vertical:

julia> [1 2 3 4;
        3 4 2 1;
        4 3 1 2;
        2 1 4 3]

La función hvcat puede ser útil cuando la serie de valores no se puede escribir a mano, por ejemplo porque está contenida (quizás con una estructura distinta) en otras variables. La sintaxis de esta función es:

hvcat(ncols, valores...)

donde ncols es el número de columnas esperado en cada fila, y valores... representa un número indefinido de argumentos (múltiplo de ncols) con los valores a organizar, ordenados "fila a fila" (como se leen en la forma abreviada). Por ejemplo (cambiando a una matriz de cadenas de texto, para que se vea con más claridad la diferencia de los argumentos):

julia> hvcat(3, "a", "b", "c", "x", "y", "z")
2×3 Matrix{String}:
 "a"  "b"  "c"
 "x"  "y"  "z"

En un ejemplo más realista los valores estarían agrupados en otra variable, como podría ser un vector. Los valores individuales de dicho vector podrían pasarse a la función hvcat mediante la técnica de splatting (añadiendo puntos suspensivos al nombre de la variable), como se indicaba en la sección sobre Agrupaciones de argumentos del capítulo 3:

julia> letras = ["a", "b", "c", "x", "y", "z"];

julia> hvcat(3, letras...)
2×3 Matrix{String}:
 "a"  "b"  "c"
 "x"  "y"  "z"

Otro caso de uso práctico de hvcat es para crear una matriz con una sola columna (pero con dos dimensiones, no como los vectores). Véase la sutil diferencia entre los dos siguientes resultados:

julia> vector = ["a", "b", "c"]
3-element Vector{String}:
 "a"
 "b"
 "c"

julia> matriz_columna = hvcat(1, "a", "b", "c")
3×1 Matrix{String}:
 "a"
 "b"
 "c"

Aunque la disposición de los valores es idéntica, el tipo de array es distinto: El primero es un Array{String, 1} (es decir, un array cuyos elementos son de tipo String con una sola dimensión), que contiente "3 elementos". Por contra, el segundo es un Array{String, 2} (con dos dimensiones), de tamaño 3×1.

Para finalizar con las matrices y las distintas formas de concatenar valores en dos dimensiones, resulta pertinente destacar la diferencia entre el uso de la coma y el punto y coma (o el cambio de línea) como separador de elementos: la coma es el separador de elementos en vectores, mientras que el punto y coma indica que el siguiente elemento se concatene con los anteriores añadiendo filas al array –sea un vector o una matriz–. Esto explica los distintos resultados de estas dos operaciones:

julia> unodos = [1, 2];

julia> [unodos; 3] # concatena el tres como otra fila
3-element Vector{Int64}:
 1
 2
 3

julia> [unodos, 3] # crea un vector añadiendo el tres
2-element Vector{Any}:
  [1, 2]
 3

La diferencia entre los separadores solo se diluye al crear un vector a partir de elementos sueltos, aunque ni siquiera en ese caso son intercambiables, pues no se pueden mezclar:

julia> [1, 2, 3] == [1; 2; 3] # Ambas expresiones son equivalentes
true

julia> [1, 2; 3]   # Pero esto no funciona
ERROR: syntax: unexpected semicolon in array expression

Arrays n-dimensionales

Los arrays con más de dos dimensiones se crean con la función cat descrita para vectores y matrices, sin ninguna forma alternativa o abreviada. Por ejemplo, la operación que habría que realizar para componer los dos sudokus como dos "capas" de una hipermatriz tridimensional es:

julia> cat(sudoku, sudoku2, dims=3)
4×4×2 Array{Int64, 3}:
[:, :, 1] =
 1  4  3  2
 2  3  4  1
 3  1  2  4
 4  2  1  3

[:, :, 2] =
 1  2  3  4
 3  4  2  1
 4  3  1  2
 2  1  4  3

Por otro lado, a partir de un conjunto de datos estructurados en un array con ciertas dimensiones se puede crear otro con dimensiones distintas pero compatibles (es decir que en conjunto pueda recoger el mismo número de elementos), a través de la función reshape. El primer argumento de esta matriz es el conjunto de datos a redimensionar, y luego siguen las dimensiones deseadas, en orden. En una (y solo una) de las dimensiones el número objetivo puede sustituirse por dos puntos, para indicar que se calcule automáticamente a partir del número de elementos y las demás dimensiones. Por ejemplo:

julia> matriz = [
           0.1 0.01 1 10;
           0.2 0.02 2 20;
           0.3 0.03 3 30
           ]
3×4 Matrix{Float64}:
 0.1  0.01  1.0  10.0
 0.2  0.02  2.0  20.0
 0.3  0.03  3.0  30.0

julia> reshape(matriz, 3,2,:) # Varias capas de 3×2
3×2×2 Array{Float64, 3}:
[:, :, 1] =
 0.1  0.01
 0.2  0.02
 0.3  0.03

[:, :, 2] =
 1.0  10.0
 2.0  20.0
 3.0  30.0

Un caso típico en el que se utiliza esta operación es cuando el conjunto de datos proviene de un archivo de texto, que se ha leído en forma de matriz a través de readdlm o de forma equivalente, que se quiere pasar a una hipermatriz con más dimensiones.

Además, reshape también puede servir de contrapartida a hvcat para crear matrices a partir de un vector de datos, cuando estos se quieren disponer "columna a columna".

Generación automatizada de arrays

Valores predefinidos

Hay algunos arrays prototípicos que se emplean a menudo, y se pueden crear de forma rápida con funciones específicas para ellos, sin tener que definir sus valores uno a uno. Por ejemplo, las funciones zeros y ones sirven para crear arrays compuestos enteramente de ceros o unos, con unas dimensiones dadas. También existen las funciones análogas trues and falses, para crear arrays con los correspondientes valores lógicos (verdadero o falso). Por ejemplo, podemos crear las siguientes matrices de tamaño 2×3 (aunque estas funciones sirven para crear arrays con cualquier número de dimensiones):

julia> zeros(2,3)
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

julia> ones(2,3)
2×3 Matrix{Float64}:
 1.0  1.0  1.0
 1.0  1.0  1.0

julia> trues(2,3)
2×3 BitMatrix:
 1  1  1
 1  1  1

julia> falses(2,3)
2×3 BitMatrix:
 0  0  0
 0  0  0

Por otro lado, la función fill permite crear un array compuesto por otro valor (no necesariamente números), que ha de pasarse como primer argumento:

julia> fill("abc", 2, 3)
2×3 Matrix{String}:
 "abc"  "abc"  "abc"
 "abc"  "abc"  "abc"

Si ya se tiene una matriz preparada para recibir los valores, se puede utilizar la función fill! (con una exclamación al final del nombre) para rellenarla con un valor dado, en lugar de tener que crear una matriz nueva.

julia> matriz = zeros(2,3)
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

julia> fill!(matriz, 0.5)
2×3 Matrix{Float64}:
 0.5  0.5  0.5
 0.5  0.5  0.5

julia> matriz
2×3 Matrix{Float64}:
 0.5  0.5  0.5
 0.5  0.5  0.5

Valores aleatorios

Hay situaciones en las que se desea crear arrays con valores aleatorios, por ejemplo para probar programas que se están desarrollando, poner ejemplos de uso, etc. En el capítulo de gráficos ya vimos el uso de la función randn para generar números aleatorios distribuidos según una normal. Por otro lado, la función rand permite generar números distribuidos uniformemente entre 0 y 1, con la misma sintaxis que randn, zeros y ones:

julia> rand(2,3)
2×3 Matrix{Float64}:
 0.521214  0.890879  0.525662
 0.586807  0.190907  0.390588

Además, tanto randn como rand generan números aleatorios aislados (escalares, no contenidos en ningún array), si no se les pasa ningún argumento:

julia> rand()
0.044818005017491114

julia> randn()
1.5491245530427917

Y además de generar números de una distribución uniforme, rand también sirve para seleccionar aleatoriamente elementos de una serie predefinida de valores (no solo números), que se le ha de pasar como primer argumento:

julia> letras = ["a","b","c","d"];

julia> rand(letras, 3)
3-element Vector{String}:
 "c"
 "b"
 "c"

Si se quiere generar estos números aleatorios (en realidad pseudoaleatorios) de forma reproducible, es decir que sean los mismos cuando se vuelva a ejecutar el programa, se puede fijar la "semilla" del algoritmo de aleatorización, con la función Random.seed! (antes hay que importar el módulo Random). Esta función toma solo un argumento, que es un número entero arbitrario (sirve cualquiera, pero ha de ser el mismo para conseguir resultados repetibles):

julia> rand() # un número aleatorio
0.8362285750521512

julia> rand() # otro número aleatorio distinto
0.04090613602769255

julia> Random.seed!(111); # fijamos semilla

julia> rand() # número repetible
0.42495556892617514

julia> rand() # siguiente número repetible
0.4288835273937086

julia> Random.seed!(111); # misma semilla

julia> rand() # mismos resultados que antes...
0.42495556892617514

julia> rand()
0.4288835273937086

Valores indefinidos

También se pueden crear arrays con valores indefinidos, con la finalidad de darles valores concretos más adelante. Esto es más eficiente que crearlos con un valor predefinido, y además permite que el array contenga cualquier tipo de datos. Veamos dos ejemplos: uno para crear una hipermatriz de números enteros, y otro para crear un vector con 3 cadenas de texto:

julia> Array{Int}(undef, 1, 3, 2)
1×3×2 Array{Int64, 3}:
[:, :, 1] =
 0  0  0

[:, :, 2] =
 0  0  0

julia> Array{String}(undef, 3)
3-element Vector{String}:
 #undef
 #undef
 #undef

En todos los casos, la función que crea el array toma como nombre Array{T}, donde T es el tipo de elemento que se quiere definir (en los ejemplos Int y String; véanse más detalles sobre los tipos en el siguiente apartado). El primer argumento de la función es siempre la palabra clave undef, y los siguientes son las dimensiones del array creado.

Otra forma de crear arrays con valores indefinidos es tomando otros arrays existentes como patrón, con la posibilidad de modificar su tipo o número de dimensiones, mediante la función similar:

julia> patron = zeros(2,3)
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

julia> similar(patron) # Otra matriz como la anterior
2×3 Matrix{Float64}:
 2.122e-314    4.24399e-314  6.36599e-314
 4.24399e-314  4.24399e-314  2.0e-323

julia> similar(patron, String) # Mismas dimensiones pero otro tipo de elemento
2×3 Matrix{String}:
 #undef  #undef  #undef
 #undef  #undef  #undef

julia> similar(patron, 1,2) # Otras dimensiones
1×2 Matrix{Float64}:
 0.0  6.90192e-310

julia> similar(patron, Int, 1, 2) # Otro tipo y dimensiones
1×2 Matrix{Int64}:
 0  139698423157409

Indexación y manipulación

Aunque en los capítulos anteriores ya se ha visto como extraer "partes" de un array (p.ej. elementos aislados, columnas...), vamos a describir más detalles y trucos para tener una visión más completa.

Es posible leer o modificar uno o varios valores de un array, indexando la posición seleccionar entre corchetes ([]), siguiendo el orden fila-columna-etc. (la primera posición se indica con el número 1). Si solo se utiliza un índice de posición, hay que tener en cuenta que los valores están internamente ordenados por columnas:

julia> mat = [1 10 0.1; 2 20 0.2; 3 30 0.3]
3×3 Matrix{Float64}:
 1.0  10.0  0.1
 2.0  20.0  0.2
 3.0  30.0  0.3

julia> mat[1, 2] # Primera fila, segunda columna de la matriz:
10.0

julia> mat[3 + 1] # Lo mismo: primer valor tras la primera columna:
10.0

Se pueden utilizar vectores de índices, para seleccionar varios valores o combinaciones de filas y columnas en la misma operación. Por ejemplo, para intercambiar la segunda y tercera filas de la matriz (completas, es decir los valores de las tres columnas para esas dos filas):

julia> # Véase que los índices de las filas se invierten al reasignarlos:
       mat[[2,3],[1,2,3]] = mat[[3,2],[1,2,3]];

julia> mat
3×3 Matrix{Float64}:
 1.0  10.0  0.1
 3.0  30.0  0.3
 2.0  20.0  0.2

Indexación mediante "rangos"

Estos conjuntos de índices se pueden escribir de forma más cómoda a través de "rangos", un tipo especial de variable que representa una serie aritmética acotada. Los rangos se definen a través de tres valores: el primero y último de la serie (a y b, respectivamente), más el "paso" o diferencia entre dos números consecutivos (s), con la sintaxis a:s:b. Por ejemplo, la serie de números impares entre 1 y 10:

julia> impares = 1:2:10
1:2:9

En este ejemplo el valor final asignado (10) no es compatible con la definición del valor inicial y el paso, por lo tanto se sustituye automáticamente por 9, el valor compatible más cercano (dentro del rango entre los valores inicial y final asignados). El conjunto de valores representados se entiende más fácilmente si el resultado se convierte a un vector, usando la función collect:

julia> collect(impares)
5-element Vector{Int64}:
 1
 3
 5
 7
 9

Los números de un rango no han de ser necesariamente enteros ni positivos, aunque es lo lógico cuando se quiere definir un conjunto de índices. Por otro lado, el paso s es un valor opcional, que por defecto se asume igual a 1. Para construir una serie ordenada de mayor a menor, además de definir los valores inicial y final en el orden adecuado, se ha de definir un paso negativo. Olvidar este detalle hace que la serie creada sea vacía. Por ejemplo, para una "cuenta atrás" de 5 a 1 (convertida a vector para más claridad):

julia> collect(5:-1:1) # Correcto
5-element Vector{Int64}:
 5
 4
 3
 2
 1

julia> collect(5:1) # Serie vacía
Int64[]

Algunos trucos útiles con rangos cuando se usan como índices son: las palabras clave begin y end hacen referencia respectivamente a la primera y la última posición/fila/columna indexable en el array manipulado; y los dos puntos aislados (:) hacen referencia a "todas" las posiciones, filas o columnas.

julia> numeros = [1, 2, 5, 10];

julia> numeros[end:-1:begin] # Serie de números invertida:
4-element Vector{Int64}:
 10
  5
  2
  1

julia> # Intercambiar las filas primera y segunda (antes tercera) de `mat`
       mat[1:2,:] = mat[[2,1],:];

julia> mat
3×3 Matrix{Float64}:
 3.0  30.0  0.3
 1.0  10.0  0.1
 2.0  20.0  0.2

Tipos de elementos

En Julia todos los objetos se caracterizan por el tipo de variable al que pertenecen. El tipo de una variable se puede extraer con la función typeof:

julia> typeof(1) # número entero
Int64

julia> typeof(1.0) # número decimal
Float64

julia> typeof("abc") # cadena de texto
String

Como ya se ha visto, los elementos contenidos en un array son siempre de un tipo de variable específico. El tipo de elementos de un array se muestra en la descripción del mismo, y se puede extraer con la función eltype. En el siguiente ejemplo tenemos un vector de elementos de tipo String:

julia> letras = ["a", "b", "c"]
3-element Vector{String}:
 "a"
 "b"
 "c"

julia> eltype(letras)
String

Este detalle de los arrays es importante, porque restringe los valores que se pueden introducir. Por ejemplo, en un vector de números enteros no se pueden introducir cadenas de texto, ni tampoco números decimales arbitrarios, aunque sí se pueden introducir números que se puedan convertir al tipo correspondiente:

julia> numeros = [1, 2, 3];

julia> numeros[1] = "cero";
ERROR: MethodError: Cannot `convert` an object of type String to an object of type Int64
[...]

julia> numeros[1] = 0.5;
ERROR: InexactError: Int64(0.5)
[...]

julia> numeros[1] = 5.0;

julia> numeros
3-element Vector{Int64}:
 5
 2
 3

Los tipos fundamentales de números reconocidos por Julia son los enteros y decimales. Cada uno de estos tipos tiene distintas representaciones internas:

• Los números enteros son los que tienen más variedad de representaciones internas. Pueden ser binarios (valores lógicos, representados por el tipo Bool), o de 8, 16, 32, 64 y 128 bits, así como de precsión arbitraria (BigInt). Los enteros entre 8 y 128 bits pueden ser con signo (Int8, Int16, ..., Int128) o sin signo (UInt8, UInt16, etc., números enteros positivos que suelen representarse con códigos hexadecimales). El tipo de entero por defecto se puede representar como el tipo Int, que es un alias de Int32 o Int64 según la arquitectura del sistema.
• Los números decimales (de coma flotante) pueden ser de 16, 32 ó 64 bits (Float16, Float32, Float64, respectivamente), o de precisión arbitraria (BigFloat). Por defecto son Float64 en todos los sistemas.

Además, existen otros tipos de números derivados de los anteriores:

• Números racionales (Rational), compuestos por un numerador y un denominador de números enteros, p.ej. 5//3.
• Números complejos (Complex), compuestos por una parte real y una imaginaria de números que pueden ser enteros (p.ej. 1 + 2im) o decimales (1.0 + 0.5im).

Finalmente, existe un tipo dedicado específicamente a representar el valor exacto de números irracionales (Irrational), como π o el número de Euler (ℯ), que funcionan de manera distinta.

Reglas de conversión entre tipos

Es útil tener en cuenta cuándo los números de un tipo se pueden convertir a otro. Comenzamos por señalar los casos más claros, según reglas matemáticas:

• Los valores lógicos (Bool) se pueden convertir a cualquier otro tipo de número entero, siendo true equivalente a 1, y false equivalente a 0.
• Los números enteros se pueden convertir a números decimales con parte decimal nula.
• Los números enteros se pueden convertir a números racionales con denominador igual a 1.
• Tanto los números enteros como los decimales se pueden convertir a complejos con parte imaginaria nula.

Además, dentro de la misma categoría existen casos en los que unas representaciones internas engloban a otras:

• Todos los números (enteros o decimales) de N bits pueden convertirse a números de la misma categoría con más bits (p.ej. Float32 a Float64, Int64 a Int128, o UInt8 a cualquier otro tipo de UInt.
• Los enteros con signo (Int8, Int16, ... Int128), si contienen valores de signo positivo, pueden convertirse a enteros sin signo (UInt8, etc.) con el mismo número de bits.

Estas reglas de conversión son transitivas; por ejemplo, si un valor lógico se puede convertir a cualquier tipo de entero, y los enteros se pueden convertir a decimales, los valores lógicos también se pueden convertir a decimales, etc.

Por otro lado, las conversiones inversas a las que se han indicado son posibles si se cumplen las condiciones adecuadas:

• Cualquier número de valor equivalente a uno o cero se puede convertir al tipo Bool (dando lugar a true si equivale a uno, y a false si es cero).
• Los números decimales con parte decimal nula se pueden convertir a enteros.
• Los números racionales cuyo numerador es múltiplo del denominador se pueden convertir a enteros.
• Los números complejos con parte imaginaria nula se pueden convertir a números decimales, de valor igual a la parte real.

Las conversiones inversas a las indicadas dentro de la misma categoría de tipos (enteros, decimales) dependen de los valores particulares.

Todas estas conversiones se realizan (o se intenta realizarlas) de forma automática cuando se asigna un valor de un tipo a un array con elementos de otro tipo distinto, y en otras situaciones donde conviene. Pero también se puede hacer explícitamente utilizando el nombre del tipo objetivo como función. Veamos algunos ejemplos:

julia> Float64(true)
1.0

julia> Rational(2)
2//1

julia> Complex(0.5)
0.5 + 0.0im

julia> UInt16(0x11)
0x0011

julia> Bool(1+0im)
true

julia> Int(8//4)
2

Sin embargo, como los ordenadores no tienen precisión infinita, puede que el resultado de una operación que teóricamente debería cumplir alguna de las condiciones necesarias para la conversión no lo haga. Por ejemplo, teóricamente sqrt(5.0)^2 debería dar como resultado el número 5.0, que se debería poder convertir a un entero. Sin embargo lo que tenemos es:

julia> Int(sqrt(5.0)^2)
ERROR: InexactError: Int64(5.000000000000001)

El error ya nos indica que el problema es que la operación no nos ha dado un número exactamente entero. Para arreglarlo lo tenemos que forzar a un entero, lo que se puede lograr con la función round (redondeo al número más cercano), así como con floor (redondeo al número inferior) ceil (redondeo al número superior) o trunc (redondeo quitando la parte decimal):

julia> cinco = round(sqrt(5.0)^2)
5.0

julia> Int(cinco)
5

Como el propósito de redondear suele ser convertir a un entero, estas funciones también permiten indicar directamente el tipo de número al que se quiere redondear (normalmente algún tipo de entero):

julia> round(Int, sqrt(5.0^2))
5

Tipos abstractos

Además de estos tipos de números que tienen una representación concreta en memoria, Julia tiene definida una jerarquía de tipos "abstractos", que permite interpretar variables de distintos tipos como elementos de un mismo "supertipo". La jerarquía de tipos numéricos en Julia es la siguiente:

Number ----------------------------------- Complex
        |
        ·- Real -------------------------- Rational
                 |
                 ·- AbstractIrrational --- Irrational
                 |
                 |
                 ·- AbstractFloat -------| BigFloat
                 |                       | Float64
                 |                       | Float32
                 |                       | Float16
                 |
                 ·- Integer -------------- Bool
                            |
                            ·- Signed  --| BigInt
                            |            | Int128
                            |            | Int64
                            |            | Int32
                            |            | Int16
                            |            | Int8
                            |
                            ·- Unsigned -| UInt128
                                         | UInt64
                                         | UInt32
                                         | UInt16
                                         | UInt8

Cuando se crea un array combinando elementos de distintos tipos, Julia escoge como tipo el "menos abstracto" (el más bajo en la jerarquía) que puede recoger todos los casos, incluyendo posibles conversiones. En la práctica, esto significa que si se combinan distintos tipos de enteros Unsigned se creará un array de UIntX con el número de bits más alto; si se introduce algún entero con signo pasará a ser un array de IntX; si hay algún cualquier otro tipo de número real será de FloatX, y si se añade algún número complejo será un array de Complex.

Por otro lado, si se juntan números y otro tipo de objetos (por ejemplo cadenas de texto), el tipo de elementos del array creado será Any, el "supertipo" abstracto que sirve para recoger cualquier tipo de objeto en Julia:

julia> unos = [1, 1.0, 1+0im, "uno"]
4-element Vector{Any}:
   1
   1.0
 1 + 0im
    "uno"

También es posible declarar explícitamente un array para que sea de un tipo (concreto o abstracto) a elección del usuario, siempre que los elementos introducidos sean compatibles con ese tipo. Si el array se crea introduciendo sus valores entre corchetes, esto se hace anteponiendo el nombre del tipo que se desea:

julia> Real[1, 2, 3]
3-element Vector{Real}:
 1
 2
 3

Si se crea mediante una función como cat o sus variantes, zeros, rand, etc., el tipo de variable deseado se puede introducir como primer argumento de la función:

julia> zeros(Real, 3)
3-element Vector{Real}:
 0
 0
 0

Si el tipo escogido es abstracto, como en los ejemplos anteriores, esto permite asignar al array resultante elementos de cualquiera de sus "subtipos".

Que un array esté definido como de un tipo abstracto no significa, sin embargo, que sus elementos individuales lo sean. Estos son siempre de tipos concretos, como se puede observar si se consultan sus valores:

julia> unos
4-element Vector{Any}:
   1
   1.0
 1 + 0im
    "uno"

julia> typeof(unos[1])
Int64

julia> typeof(unos[2])
Float64

julia> typeof(unos[3])
Complex{Int64}

julia> typeof(unos[4])
String

Mutabilidad de los arrays

Una característica importante de los arrays es que son un tipo de objeto mutable, es decir que sus contenidos se pueden modificar. Esto es lo que permite un manejo eficiente de los mismos, como reemplazar los valores de algunas celdas por otros sin tener que crear un array nuevo, y operaciones de "rellenado" como fill!, etc. Sin embargo, también puede dar lugar a que un array se modifique sin haberlo esperado, si no se tiene cuidado al operar con ellos. Para evitar este tipo de sorpresas conviene conocer cómo funciona la asignación de variables. La situación habitual en la que se da este problema es cuando un array se reasigna a otra variable. Por ejemplo:

julia> sa = [1, 2, 3];

julia> sb = sa; # Creamos otro array `sb` "igual a `sa`"

julia> sa[1] = 0; # Ahora modificamos `sa`...

julia> sa = sa * 10; # Volvemos a cambiar `sa`

julia> sa # Vemos cómo ha quedado `sa`:
3-element Vector{Int64}:
  0
 20
 30

El resultado de sa coincide con el esperado, pero si ahora volvemos a sb, quizás uno no esperaría esto:

julia> sb
3-element Vector{Int64}:
 0
 2
 3

Una forma de entender lo que pasa en este ejemplo es considerar que las variables sa, sb no son lo mismo que los objetos contenidos en ellas (en este caso los arrays), sino meras referencias, una especie de "etiquetas" que pueden asignarse de forma independiente, e incluso redundante a los diversos objetos que hay en el espacio de trabajo. La siguiente figura muestra gráficamente lo que ocurre en cada una de las operaciones.

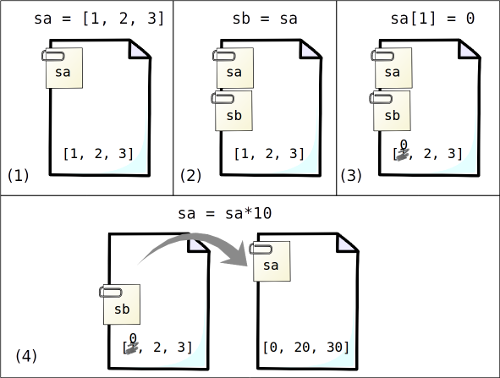
Como los arrays son elementos mutables, al hacer que sb se identifique con sa, los cambios realizados a una de las variables afecta también a la otra –a no ser que una de las variables se reasigne, como ocurre en el cuarto paso–.

Esta situación no ocurre solo al asignar arrays explícitamente, como en el ejemplo mostrado. Un caso común se da al pasar arrays como argumentos de funciones, ya que aunque en el código de la función se use otro nombre, lo que se le pasa es el array original, y las modificaciones que se hagan sobre él se reflejarán también fuera de la función.

Evitar mutaciones inesperadas

Estas situaciones se pueden evitar usando copias de los arrays cuando se asignan a distintas variables. Cuando el array es un vector, la forma más concisa de hacer una copia del mismo es "subindexando" todos sus elementos, como sigue:

julia> sa = sb[:] # Redefinimos `sa` como un vector con los valores de `sb`
3-element Vector{Int64}:
 0
 2
 3

julia> sa[1] = 1; # Los cambios en `sa`, ya no se aplican a `sb`

julia> sa
3-element Vector{Int64}:
 1
 2
 3

julia> sb
3-element Vector{Int64}:
 0
 2
 3

Para cualquier tipo de array también se puede utilizar la función copy o deepcopy. La diferencia entre ambas se oberva cuando los elementos contenidos en el array copiado son también mutables, como un array de arrays. Por ejemplo:

julia> vectores = [[1,2],[3,4]]
2-element Vector{Vector{Int64}}:
 [1, 2]
 [3, 4]

julia> copia_vectores = copy(vectores);

julia> copia_vectores[1] = zeros(3); # Reemplazamos el primer vector

julia> copia_vectores
2-element Vector{Vector{Int64}}:
 [0, 0, 0]
 [3, 4]

julia> vectores # El array original sigue intacto:
2-element Vector{Vector{Int64}}:
 [1, 2]
 [3, 4]

julia> copia_vectores[2][1] = 0; # Pero si hacemos cambios a otro nivel...

julia> copia_vectores
2-element Vector{Vector{Int64}}:
 [0, 0, 0]
 [0, 4]

julia> vectores # ... `copy` no ha evitado la mutación
2-element Vector{Vector{Int64}}:
 [1, 2]
 [0, 4]

Por otro lado, si usamos deepcopy en lugar de copy sí que se evitan las modificaciones en todos los niveles:

julia> vectores = [[1,2],[3,4]]
2-element Vector{Vector{Int64}}:
 [1, 2]
 [3, 4]

julia> copia_vectores = deepcopy(vectores);

julia> copia_vectores[2][1] = 0;

julia> copia_vectores
2-element Vector{Vector{Int64}}:
 [1, 2]
 [0, 4]

julia> vectores
2-element Vector{Vector{Int64}}:
 [1, 2]
 [3, 4]

Forzar la mutación

También se puede dar la situación inversa, cuando se quiere hacer una referencia a parte de un array y operar con ella de forma que los cambios se apliquen al original. Por ejemplo, supongamos que queremos modificar la última columna de una matriz rellenándola de otros valores:

julia> matriz = zeros(2,3)
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

julia> fill!(matriz[:, 3], 0.5)
2-element Vector{Float64}:
 0.5
 0.5

julia> matriz
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

Esto no ha funcionado, porque matriz[:, 3] es vector en el que se ha copiado de la tercera columna de matriz, lo mismo que sb[:] contenía una copia de sb en el ejemplo de la sección anterior.

La forma de trabajar con una parte del array sin hacer una copia es mediante la función view –o para mayor comodidad, con la macro^[1] @view, que permite utilizar un código más semejante al usado cuando se trabaja con copias–:

julia> matriz = zeros(2,3)
2×3 Matrix{Float64}:
 0.0  0.0  0.0
 0.0  0.0  0.0

julia> ultima_columna = @view matriz[:, 3]
2-element view(::Matrix{Float64}, :, 3) with eltype Float64:
 0.0
 0.0

julia> fill!(ultima_columna, 0.5)
2-element view(::Matrix{Float64}, :, 3) with eltype Float64:
 0.5
 0.5

julia> matriz
2×3 Matrix{Float64}:
 0.0  0.0  0.5
 0.0  0.0  0.5

Manipulación de las dimensiones

Además del tipo de variables contenidas, los arrays tienen unas dimensiones determinadas, por lo que en general no se puede acceder a posiciones fuera de esas dimensiones, ni para leerlas ni para asignarles valores en ellas. En el caso particular de los vectores, sin embargo, hay múltiples funciones para redimensionarlos (sin tener que crear nuevas variables):

• resize(v, n) para cambiar la longitud del vector v a n elementos (añadiendo valores indefinidos si n es mayor que la longitud original de v).
• push!(v, x, y...) para añadir uno o más elementos (x, y, etc.), al final del vector v.
• pushfirst!(v, x, y...) para añadir uno o más elementos (x, y, etc.) al principio del vector v.
• insert!(v, i, x) para insertar el elemento x en la posición i del vector v (moviendo la posición de los siguientes elementos).
• append!(v, w) para extender el vector v añadiéndole el conjunto de datos w (otro vector u otro tipo de colección) al final.
• prepend!(v, w) para extender el vector v añadiéndolo los datos de w al principio.
• pop!(v) para extraer y eliminar el último elemento del vector v.
• popfirst!(v) para extraer y eliminar el primer elemento del vector v.
• deleteat!(v, indices) para eliminar los elementos señalados en indices del vector v.
• splice!(v, indices, w) para eliminar los elementos señalados en indices del vector v, y opcionalmente poner los elementos de w en su lugar (semejante a una combinación de deleteat! e insert!).
• empty!(v) para eliminar todos los elementos del vector v.

En lo que respecta a matrices y arrays multidimensionales en general, la única manera de añadir elementos, filas, columnas, etc. a un array es crear uno nuevo mediante cat o las operaciones relacionadas que se han explicado en la primera sección de este capítulo.

Otro tipo de manipulación que se puede hacer con los arrays es redimensionarlos o reordenar sus dimensiones. Un ejemplo que ya hemos visto al principio de este capítulo es la función reshape, con la que se crea un array con nuevas dimensiones (manteniendo el número total de elementos).

Por otro lado, la función permutedims sirve para cambiar el orden de las dimensiones, sin cambiar el número de elementos en cada una. El primer argumento de estas funciones es el array a reorganizar, al que siguen los índices de las dimensiones originales, en el orden en el que se quieren dejar (organizados en una "tupla", es decir entre paréntesis). Por ejemplo, el siguiente código intercambia la primera y la tercera dimensión de un array tridimensional, dejando la segunda en el mismo lugar:

julia> numeros = cat([1 10; 2 20; 3 30],
       [0.1 0.01; 0.2 0.02; 0.3 0.03],
       dims=3)
3×2×2 Array{Float64, 3}:
[:, :, 1] =
 1.0  10.0
 2.0  20.0
 3.0  30.0

[:, :, 2] =
 0.1  0.01
 0.2  0.02
 0.3  0.03

julia> permutedims(numeros, (3, 2, 1))
2×2×3 Array{Float64, 3}:
[:, :, 1] =
 1.0  10.0
 0.1   0.01

[:, :, 2] =
 2.0  20.0
 0.2   0.02

[:, :, 3] =
 3.0  30.0
 0.3   0.03

Los elementos de los arrays resultantes de estas operaciones son referencias directas a los elementos de los originales. Esto significa que los cambios que se hagan en los arrays transformados también modificarán los primeros.

Broadcasting

Cuando se quiere aplicar una misma operación a todos los elementos de un array, o a los de varios arrays del mismo tamaño, se puede escribir un bucle que recorra sus distintos elementos; pero también existe una forma especial de operar, conocida como broadcasting, que tiene una sintaxis compacta y muy práctica.

Vamos a ver un ejemplo con la operación para calcular el módulo de un vector de dos elementos, que se usó para introducir esta forma de operar en el capítulo 2. Primero vemos los resultados de la operación con escalares:

julia> x = 0.5; y = 1.2;

julia> sqrt(x^2 + y^2)
1.3

julia> x = 3; y = 4;

julia> sqrt(x^2 + y^2)
5.0

Si los dos valores de x y los dos de y los tuviéramos en sendos vectores, podríamos hacer la operación con todos sus elementos a la vez, utilizando la sintaxis de broadcasting, que esencialmente consiste en añadir un punto tras los nombres de las funciones, o antes de los operadores. El resultado lo asignaremos a otro vector m definido de antemano, para mostrar como esas "operaciones con punto" también incluyen la asignación de valores a arrays existentes:

julia> x = [0.5, 3]; y = [1.2, 4]; m = zeros(2);

julia> m .= sqrt.(x.^2 .+ y.^2)
2-element Vector{Float64}:
 1.3
 5.0

A esta técnica se le llama broadcasting porque consiste en transmitir una operación escalar a todos los elementos de los operandos, y también porque los valores escalares (p.ej. el 2 que se utiliza como exponente en el código anterior) se aplican a todos los elementos de los arrays, como si ellos mismos estuviesen en arrays de la misma dimensión, con el mismo valor en todas las celdas. Además, los arrays también se pueden comportar como si sus dimensiones "unitarias" se ampliasen en la medida necesaria. Esto se ve mejor con otro ejemplo:

Imaginemos que queremos multiplicar cada elemento del vector columna [1, 2, 3] por cada uno del vector fila [4 5], a la manera de un producto tensorial. Una forma de hacerlo sería multiplicar dos matrices de tamaños congruentes, cuyas filas y columnas fuesen réplicas de esos vectores. Por ejemplo, usando la función repeat:

julia> a = [1, 2, 3]
3-element Vector{Int64}:
 1
 2
 3

julia> b = [4 5]
1×2 Matrix{Int64}:
 4  5

julia> ma = repeat(a, 1, 2) # filas repetidas una vez, columnas dos veces
3×2 Matrix{Int64}:
 1  1
 2  2
 3  3

julia> mb = repeat(b, 3, 1) # filas repetidas tres veces, columnas una vez
3×2 Matrix{Int64}:
 4  5
 4  5
 4  5

julia> ma .* mb # Multiplicación con broadcasting
3×2 Matrix{Int64}:
  4   5
  8  10
 12  15

Sin embargo, esto no es necesario, ya que el mecanismo de broadcasting realiza los cálculos equivalentes a partir de los vectores originales, de forma más eficiente:

julia> a .* b
3×2 Matrix{Int64}:
  4   5
  8  10
 12  15

Normalmente, para hacer una operación "elemento a elemento" con los arrays es necesario hacerlo mediante broadcasting, ya que de lo contrario se intentará hacer la operación considerando el array completo como un objeto individual. A veces puede querer hacerse eso mismo; por ejemplo se pueden comparar dos arrays en su conjunto, que no es lo mismo que comparar los elementos individuales y guardar las comparaciones en un array de resultados:

julia> [1, 2, 3] == [1, 2, 4] # comparación de los arrays
false

julia> [1, 2, 3] .== [1, 2, 4] # comparación de sus elementos
3-element BitVector:
 1
 1
 0

Cuando se combinan varias operaciones en la misma línea, puede resultar engorroso y poco estético añadir puntos a todas las funciones y operadores. Un truco para escribir código más "limpio" es utilizar la macro @., que convierte en operaciones con boradcasting todo lo que sigue en esa línea, por ejemplo, la operación del primer ejemplo de esta sección se puede escribir de las siguientes dos maneras:

m .= sqrt.(x.^2 .+ y.^2)
@. m = sqrt(x^2 + y^2)

Operaciones matriciales

Las matrices numéricas son solo un tipo particular de arrays, pero especialmente relevante, ya que son un elemento fundamental del álgebra lineal. Debido a su importancia, hay una gran cantidad de operaciones matemáticas específicas para este tipo de variables, que no son aplicables a arrays no numéricos o de más dimensiones. Sí se pueden usar, sin embargo, con vectores, con los que a estos efectos se opera como si fueran matrices de una sola columna.

Las cálculos matriciales incluyen las operaciones algebraicas elementales (suma, resta, multiplicación, división, potenciación por un escalar...), cálculos en el espacio de los números complejos, y cálculos numéricos como exponenciales, logaritmos, funciones trigonométricas, etc. En el caso particular de la suma y la resta de matrices, el resultado es el mismo que si se hace "elemento a elemento":

julia> m = [4 1 -1; 1 2 1; -1 1 2]
3×3 Matrix{Int64}:
  4  1  -1
  1  2   1
 -1  1   2

julia> m2 = ones(3, 3)
3×3 Matrix{Float64}:
 1.0  1.0  1.0
 1.0  1.0  1.0
 1.0  1.0  1.0

julia> m + m2 # suma matricial
3×3 Matrix{Float64}:
 5.0  2.0  0.0
 2.0  3.0  2.0
 0.0  2.0  3.0

julia> m .+ m2 # suma de elementos
3×3 Matrix{Float64}:
 5.0  2.0  0.0
 2.0  3.0  2.0
 0.0  2.0  3.0

Para cualquier otra operación, no tiene nada que ver hacer el cálculo con la matriz completa o con sus elementos individuales:

julia> m * m2 # producto de matrices
3×3 Matrix{Float64}:
 4.0  4.0  4.0
 4.0  4.0  4.0
 2.0  2.0  2.0

julia> m .* m2 # producto de los elementos
3×3 Matrix{Float64}:
  4.0  1.0  -1.0
  1.0  2.0   1.0
 -1.0  1.0   2.0

julia> exp(m) # exponencial de la matriz
3×3 Matrix{Float64}:
  82.9048  22.8424   -22.8424
  22.8424  17.2315     2.85401
 -22.8424   2.85401   17.2315

julia> exp.(m) # exponencial de los elementos
3×3 Matrix{Float64}:
 54.5982    2.71828  0.367879
  2.71828   7.38906  2.71828
  0.367879  2.71828  7.38906

Matrices transpuestas

La transposición de matrices es una operación habitual en el álgebra lineal. En una sección anterior ya hemos visto cómo intercambiar filas por columnas en matrices de cualquier tipo con la función permutedims. En el caso de las matrices numéricas, esta operación se realiza de manera mucho más eficiente a través de la función transpose.

Una diferencia fundamental entre usar transpose y permutedims con matrices, es que aunque transpose guarde el resultado en una nueva variable, en realidad no crea una matriz nueva, sino que la variable que representa la matriz transpuesta mantiene una referencia a la original. Esto significa que los cambios que se hagan en cualquiera de las dos afectan a la otra. Por ejemplo:

julia> m = [1 2 3; 4 5 6]
2×3 Matrix{Int64}:
 1  2  3
 4  5  6

julia> mt = transpose(m)
3×2 transpose(::Matrix{Int64}) with eltype Int64:
 1  4
 2  5
 3  6

julia> m[1, 2] = 20; # cambiamos un elemento de `m`

julia> m
2×3 Matrix{Int64}:
 1  20  3
 4   5  6

julia> mt # y el cambio también afecta a `mt`
3×2 transpose(::Matrix{Int64}) with eltype Int64:
  1  4
 20  5
  3  6

Las matrices transpuestas se suelen usar en para resolver problemas algebraicos (factorización, inversión...) que implican matrices con números reales. Cuando las matrices pueden contener números complejos, lo que se suele usar son sus transpuestas conjugadas, en las que la parte imaginaria aparece con el signo opuesto. La transpuesta conjugada (también llamada matriz adjunta) se obtiene con la función adjoint, o más concisamente escribiendo un apóstrofe tras la matriz:

julia> mc = [1 -2im; 1+0.5im 0]
2×2 Matrix{ComplexF64}:
 1.0+0.0im  0.0-2.0im
 1.0+0.5im  0.0+0.0im

julia> mc'
2×2 adjoint(::Matrix{ComplexF64}) with eltype ComplexF64:
 1.0-0.0im  1.0-0.5im
 0.0+2.0im  0.0-0.0im

julia> adjoint(mc)
2×2 adjoint(::Matrix{ComplexF64}) with eltype ComplexF64:
 1.0-0.0im  1.0-0.5im
 0.0+2.0im  0.0-0.0im

Cuando se trabaja con matrices de números reales, la transpuesta conjugada es lo mismo que la transpuesta "a secas", por lo que se suele usar la sintaxis con el apóstrofe para que el código sea más conciso.

Matrices diagonales

En muchos cálculos se hace uso de matrices diagonales, es decir matrices que son nulas en todos los elementos menos en la diagonal principal. En el módulo LinearAlgebra hay un tipo especial de matrices para este propósito, llamado Diagonal. Una matriz de este tipo se puede construir fácilmente a partir de un vector con los valores a incluir en la diagonal:

julia> using LinearAlgebra

julia> Diagonal([1,2,3])
3×3 LinearAlgebra.Diagonal{Int64, Vector{Int64}}:
 1  ⋅  ⋅
 ⋅  2  ⋅
 ⋅  ⋅  3

Las posiciones fuera de la diagonal se interpretan como ceros, pero en realidad no "existen" (es decir, no tienen representación en memoria), por lo que no se pueden modificar.

Una matriz diagonal particularmente importante es la "matriz identidad", equivalente a la unidad en el álgebra de matrices, cuya diagonal está compuesta enteramente de unos. Una matriz diagonal de tamaño n×n podría construirse como Diagonal(ones(n)). Pero también existe un tipo especial para esta matriz particular, que se construye con la letra I mayúscula (la forma habitual de representar la matriz identidad).

I representa una matriz identidad de cualquier tipo numérico y tamaño, de tal manera que se puede utilizar en distintas operaciones algebraicas sin añadirle más detalles. Por ejemplo, supongamos que queremos definir una matriz que, al multiplicarla por un vector cualquiera, dé como resultado la proyección de dicho vector sobre el plano perpendicular a otro vector (unitario) n. Esa matriz está definida como la matriz identidad menos el producto tensorial de n por sí mismo. Esto se puede escribir como I - n*n', sin tener que especificar el tamaño de I. Veamos un caso particular:

julia> n = [1/3, 2/3, 2/3];

julia> I - n * n'
3×3 Matrix{Float64}:
  0.888889  -0.222222  -0.222222
 -0.222222   0.555556  -0.444444
 -0.222222  -0.444444   0.555556

Para crear una matriz identidad con un tipo de número y tamaño concreto (no necesariamente cuadrada), se puede utilizar la siguiente sintaxis:

julia> Matrix(1.0 * I, 3, 5) # Numeros decimales (como 1.0), de tamaño 3×5
3×5 Matrix{Float64}:
 1.0  0.0  0.0  0.0  0.0
 0.0  1.0  0.0  0.0  0.0
 0.0  0.0  1.0  0.0  0.0

(Si se cambia el 1.0 de este ejemplo por cualquier otro número, las entradas de la diagonal aparecerán multiplicadas por ese número.)

A veces puede interesar también crear matrices "pseudo-diagonales", en las que las diagonales con valores no nulos no sean la central. Para esto se puede usar la función diagm, que toma como argumentos parejas de índices y vectores, del tipo d => v, donde d es el índice de una diagonal, y v el vector con los valores de la misma. La diagonal central tiene como índice 0, las diagonales superiores tienen índices positivos, y las inferiores índices negativos. El resultado es una matriz cuadrada, con el tamaño necesario para contener los valores introducidos. Por ejemplo:

julia> pseudodiagonal = diagm(2 => [1, 2, 3], -1 => [4,5])
5×5 Matrix{Int64}:
 0  0  1  0  0
 4  0  0  2  0
 0  5  0  0  3
 0  0  0  0  0
 0  0  0  0  0

Complementariamente, la función diag(m, i) sirve para extraer la diagonal con índice i de la matriz m (por defecto la diagonal principal, si no se especifica ningún índice):

julia> diag(pseudodiagonal, -1)
4-element Vector{Int64}:
 4
 5
 0
 0

Otras operaciones

El álgebra de matrices es un campo muy amplio, del que solo hemos visto aspectos relacionados con la creación de las matrices y operaciones elementales. Una presentación completa de las operaciones y funciones disponibles excede en mucho el enfoque de esta guía, pero se puede encontrar la referencia completa en la página sobre álgebra lineal del manual oficial de Julia.

Sumario del capítulo

En este capítulo hemos visto cómo trabajar con arrays (vectores, matrices y conjuntos de datos multidimensionales en general). En particular, se ha explicado:

• Cómo crear arrays de distintas dimensiones con las funciones cat, hcat, vcat, hvcat, o mediante la sintaxis abreviada con corchetes (a partir de valores concretos), así como algunas formas de hacer arrays con valores predefinidos (a través de zeros, ones, trues, falses, fill o fill!), o con valores indefinidos (usando constructores con undef).
• La definición de algunas matrices especiales: matrices diagonales con diagm y de tipo Diagonal, y la matriz identidad con I; uso de la función diag para extraer diagonales de una matriz.
• Cómo añadir y eleminar elementos de vectores (sin crear nuevas variables) mediante las funciones push!, pushfirst!, insert!, append!, prepend!, pop!, popfirst!, deleteat!, splice! y empty!.
• Cómo reorganizar las dimensiones de arrays mediante las funciones reshape y permutedims – y en el caso de matrices numéricas, con transpose y adjoint (o con el operador ' como forma abreviada de adjoint).
• La sintaxis para "subindexar" arrays a través de índices numéricos y rangos, y el uso de la macro @view para que los subarrays creados hagan referencia a los valores originales.
• La sintaxis para aplicar broadcasting a las operaciones con arrays (funciones y operadores "con punto").

Además, se han explorado otros aspectos de Julia no estrictamente asociados a los arrays, aunque tienen especial relevancia en los mismos:

• Los distintos tipos de variables, y en particular la familia de tipos numéricos: las relaciones jerárquicas entre ellos, las posibilidades de conversión entre tipos, y cómo definir los arrays para manejar distintos tipos de variables.
• Cómo funciona la asignación de objetos a variables en Julia, las implicaciones que esto tiene sobre los objetos mutables (como los arrays), y el uso de las funciones copy y deepcopy para evitar mutaciones no deseadas al reasignar objetos a distintas variables.

Finalmente, también se han explicado algunas funciones del módulo Random para la generación de números aleatorios (p.ej. rand, rand!, randn y randn!), y la configuración de la "semilla" (Random.seed!) para asegurar la reproducibilidad de los resultados cuando se usan esas funciones.